Nullstellen Polynom 3. Grades - Koeffizientenvergleich

(x-2)*(x+2)*(x+3)=0=(x-a)*(x-b)*(x-c)=x^3+3x^2-4x-12  für x=a,b,c

Koeffizientenvergleich, es wird eine Nullstelle gesucht, x=a

-ax^2-bx^2-cx^2+abx+bcx+acx-abc+x^3=0

x^3=1xxx    -bx^2-cx^2-ax^2=3xx      abx+bcx+acx=-4x    -abc=-12

(x^2-xb-xc+cb)(x-a)=0, x^2-xc-xb+cb=0 bei a=x

-b-c-a=3    x^2-xb-xc+cb=y    ab+bc+ac=-4 daraus folgt für x=a  a^2-ab-ac+cb=y

die beiden letzten Gleichungen addieren

a^2+2bc=y-4

a^3+2abc=ay-4a

Koeffizientenvergleich Ergebnisse einsetzen für x=a

a^3+24=a*(a^2-ab-ac+cb)-4a

24=-a^2*b-a^2*c+abc-4a

-12=a^2*b+a^2*c+4a

-12=a*(ab+ac+4)

ab+bc+ac=-4 ab+ac=-4-bc

12=abc

a*(b+c)=-4-bc
-4=-4
a*(-a-3)=-4-bc
a^3+3a^2-4a-12=0

Problem/Ansatz:

auf diese Berechnungen aufbauend, siehe Link: https://www.mathelounge.de/1095319/integration-umkehrfunktion-differentiation-umkehrfunktion

f(x)=x^3-2x    f'(x)=3x^2-2            Umkehrfunktion: f'_u=+- (x+2)^0.5/(3)^0.5    F(x)=1/4x^4-x^2      Umkehrfunktion: F_u1=+-(2-2*(x+1)^0.5)^0.5  und F_u2=+-2^0.5*((x+1)^0.5+1)^0.5
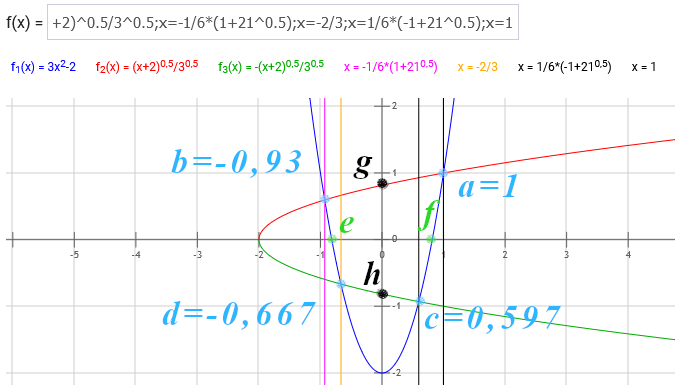
Berechnung der von der Ableitungsfunktion und ihrer Umkehrfunktion eingeschlossenen Fläche: Schnittpunkte:
3x^2-2=+-(x+2)^0.5/3^0.5    a=1, b=-1/6*(1+(21)^0.5), c=1/6*(-1+(21)^0.5), d=-2/3

Berechnung der eingeschlossenen Fläche:

Integral von -(3b^2-2) bis (3a^2-2)  (x+2)^0.5/3^0.5 dx=2-0,425758=1,57422=

Integral von (3a^2-2) bis (3c^2-2) (x+2)^0.5/3^0.5 dx=-2*(c^3-a^3)

Integral von -(3d^2-2) bis (3c^2-2) (x+2)^0.5/3^0.5 dx=1,610943-0,59259=1,01835=

Integral von (3d^2-2) bis (3b^2-2) (x+2)^0.5/3^0.5 dx=2*(d^3-b^3)

.....auch damit wurde gezeigt, daß die Integrale richtig berechnet wurden......

1,57422+1,01835= 2,59257=B      ()^2=6,72142        B^2=A

Berechnung der von der Integrationsfunktion und ihrer Umkehrfunktion eingeschlossenen Fläche mit modifizierter Integrationsgrenze:

(x+2)^0.5/3^0.5=1/4x^4-x^2   dies ist die modifizierte Integrationsgrenze..... a=2,22658   b=-1

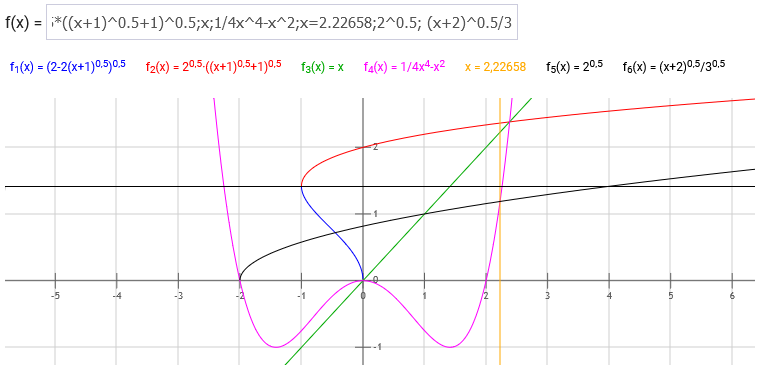
Integral von (2-2(b+1)^0.5)^0.5 bis (1/4a^4-a^2)  (2^0.5*((x+1)^0.5+1)^0.5) dx=5,975835+0,75425=6,73=A

Vergleiche: 6,73 ist fast genau 6,72142

den Fehlerwert würde ich auf das Rechnen mit ungenauen Dezimalstellen festlegen

Die gesamte Rechnung ist jedoch von der modifizierten Integrationsgrenze abhängig, damit steht und fällt alles.

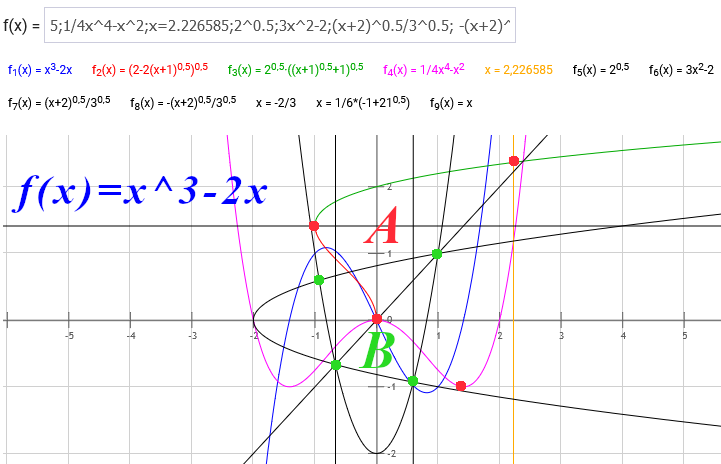
ein Beispiel, daß meine Integrale korrekt berechnet wurden:

Integral von 0 bis 2 -(1/4x⁴-x²) dx=1,066667= Integral von
(2-2(b+1)^0.5)^0.5 bis (1/4a⁴-a²) (2^0.5*((x+1)^0.5+1)^0.5) dx mit a=beliebig, größer 0 und b=-1, x=0   siehe www.Integralrechner.de

dies ergibt sich durch die Spiegelung der Funktionen an der Achse y=x, es wurden ja die Umkehrfunktionen ermittelt

Sollte Jemanden ein Fehler in diesen Berechnungen auffallen, dann wäre es schön, sollte man mich per Mail / Kontaktformular informieren! Dankeschön!